Debugging CGAffineTransform Scale to Zero Animations on iOS | Blog

I was recently working on an application which required me to display an animation which scales a UIView down to zero. The approach I took was to apply a CGAffineTransform (with scale factor set to zero) to the UIView in a UIView.animate() block. However, when I implemented this, the view did not animate but just disappeared from the UI. The problem turned out to be something which is not really obvious from the iOS docs and hence I decided to write up this post in the hope that it will help others.

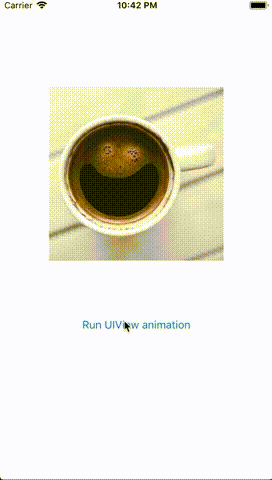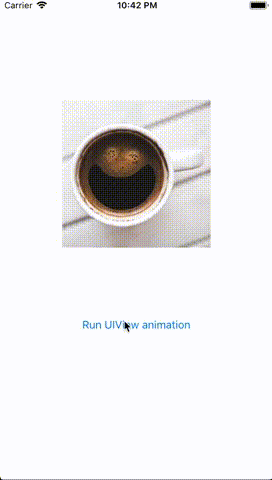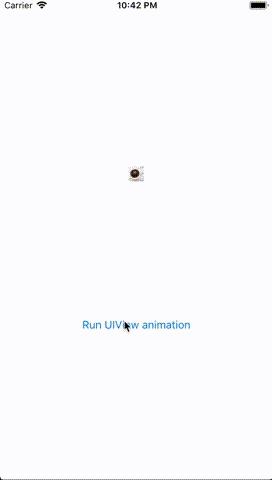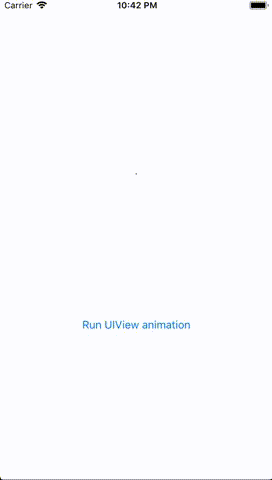
This is the behaviour I wanted to implement:

This is the code I initially wrote up to do this:

let someView = UIView()
let scaleTransform = CGAffineTransform(scaleX: 0, y: 0)
UIView.animate(withDuration: 3.0, animations: {
    view.transform = scaleTransform
})

Here is the actual result of the above code on iOS 12.0 (quick note — this seems to behave differently on different iOS versions):

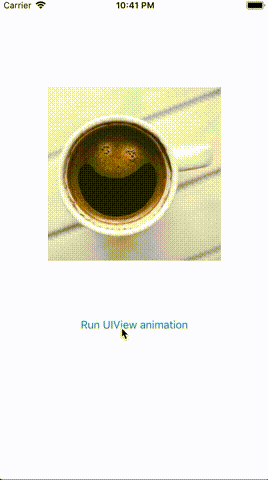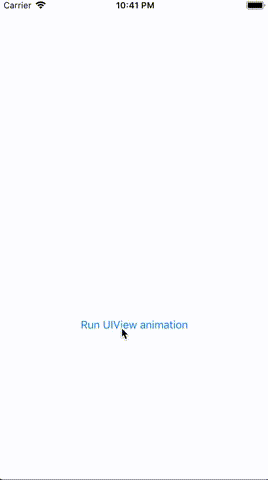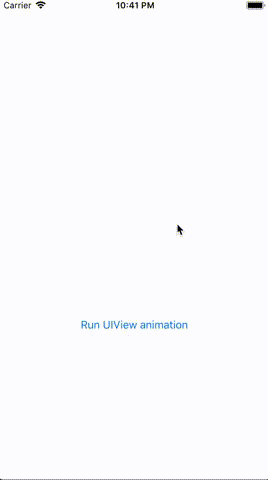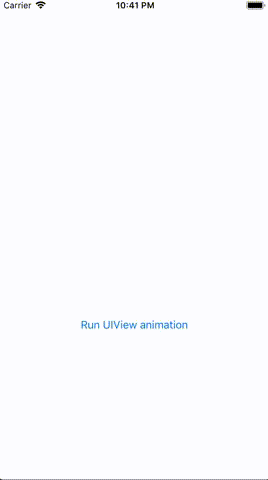
This is an intriguing problem since, based on the iOS docs, this should have worked. After digging into this by creating a sample app and reading up on some “Affine Transform” math, I was able to track down the root cause.

For the impatient, here is a quick explanation of the root cause and a potential solution (a more detailed explanation follows this):

To perform a CGAffineTransform animation, iOS first decomposes both, the scaleTransform matrix and the current UIView transform (lets call this currentTransform which in our case is the identity transform) into its constituents — scale, shear, rotate and translate.
It then interpolates over each of these values from the currentTransform to scaleTransform, internally creating a new CGAffineTransform for each animation frame.
Finally, it applies these generated transforms to the UIView at the required frame rate to display the animation.
The root cause of our problem lies with the math to decompose a CGAffineTransform matrix. If the scale factor is zero, the math involved tries to divide by zero (which is undefined / infinity) and, as a result, the iOS animation behaves unpredictably.

A potential solution (and the one I used in my implementation) was to use a really small but non-zero value for the scale factor (e.g. 0.001) and then set the UIView.isHidden = true when the animation completes so that the view is completely hidden from the UI.

Detailed explanation:

Let us now move on to a more detailed explanation on why iOS decomposes the CGAffineTransform matrix, the math used to do this and how that leads to a problem.

A quick recap of the CGAffineTransform matrix and UIView.animate() methods:

CGAffineTransform matrix

The CGAffineTransform is a 3x3 matrix where a, b, c, d together define the scale, shear and rotation while tx and ty define translation. Of these, specifically, a and d play a part in defining the scale (refer below image). This is how a standard CGAffineTransform matrix looks like:

By default, the UIView.transform property is set to an identity matrix (CGAffineTransform.identity) and applying any of scale / shear / rotate / translate operations basically involves multiplying this identity matrix with the required matrix.

UIView.animate()

UIView.animate() interpolates values for the animated properties from the initial value (i.e. value before animation) to the final value and applies this to the UIView for each animation frame over the specified duration. For example, the following code will interpolate x and y from 0 to 10 and keep applying it to the someView.center property at the required frame rate so that the user sees the someView animate to the new position over a duration of 3 seconds.

let someView = UIView()
someView.center = CGPoint(x: 0, y: 0)
UIView.animate(withDuration: 3.0, animations: {
    someView.center = CGPoint(x: 10, y: 10)
})

With this information, consider the original (buggy) code snippet (which animates the UIView.transform property). At face value, it is easy to assume that the iOS animation will just interpolate the identity matrix [[1,0,0], [0,1,0], [0,0,1]] (initialTransform) to [[0,0,0], [0,0,0], [0,0,1]] (scaleTransform) by interpolating each value of the matrix. Something like:

CGAffineTransform animation interpolation assumption

To test if that is what actually happens, I put together a sample iOS application. This application uses a CGAffineTransform to rotate a UIView (I used rotation in the sample since the problem with our assumption is clearly demonstrated with this). The sample application works as follows:

Tapping on the “Run UIView animation” button runs the iOS animation to rotate the image by 160 degrees by generating a CGAffineTransform rotation matrix and applying it in a UIView animation block. (The intention is to understand how iOS internally does this).
Moving “Affine Transform Matrix Interpolation” slider generates intermediate matrices by interpolating each value of the matrix (similar to the what we discussed in the assumption) from the identity transform to a 160 degree rotation transform and applies it to the image.
Moving the “Angle Interpolation” slider generates intermediate matrices by interpolating over the angle (0 to 160 degrees) and apples it to the image.

This is how the sample application works:

Notice that the intermediate frames in the actual iOS animation generated by tapping the “Run UIView animation” button look the same as the ones generated by “Angle Interpolation” where as those generated by interpolating each value of the CGAffineTransform matrix looks different and is not the expected behaviour. For this reason, when animating the UIView.transform property, iOS actually: decomposes the initial CGAffineTransform into its components values (scale, shear, rotation, translation etc.), then interpolates over each of these values, constructs a new CGAffineTransform matrix for each animation frame and applies it to the UIView.transform property.

Now, to debug further, lets look at the math used for decomposing the CGAffineTransform matrix. The math below is for the case when we scale, shear and rotate (in that order). Also, we can ignore translation (tx, ty) for this example since those values do not impact scale / shear / rotate.

This means, the iOS SDK needs to divide by a to calculate the rotation angle and the shear factor. Now, If s (i.e. scale) is zero, a becomes zero (refer #1 above) and produces undefined results. As a result, the matrix decomposition fails and the iOS animation system produces unpredictable results.

Now, that we have the root cause, let us move on to the solution. To display a animation where the UIView needs to be scaled to zero, I suggest the following:

Using a very small but non-zero scale factor when creating the final CGAffineTransform for the animation.
On completion of the animation, setting the UIView.isHidden property to true so the UIView is hidden from the user.

In my case, I was able to make the animation work as expected by using a scale factor of 0.001 (i.e. CGAffineTransform(scaleX: 0.001, y: 0.001)). To see how this looks in an iOS app, please check the “expected behaviour” GIF which is the very first image in this post.

Wrapping up: in this post, we discussed how the internal workings of UIView.animation() and the math to decompose a CGAffineTransform matrix together lead to the “scale to zero” animation to fail unpredictably on iOS. We also discussed a potential solution / work around for this problem.

Thanks for taking the time to read this post. Hope you found it interesting and that it helps others facing a similar problem.

Happy coding!

References: